Measuring Water Table Depth
During the Mn/ROAD 1999 reconstruction project, each of the five reconstructed cells had a monitoring well located at the centerline (Sensor Location Plans). Monitoring wells allow tracking of the water table elevations found directly below the pavement. Wells were installed at the top of the subgrade prior to placing the base course, and extend down approximately 14 feet. Two of the five reconstructed cells have automated pressure transducers installed in them for measuring the water table depth. The remaining three cells have both pressure transducers and hollow filled coaxial cable for measuring water table depth (Installation Photos). Manual data is collected from existing standpipes located in the shoulder of each cell. Automated water table measurements will be compared to manual measurements to determine accuracy and reliability of each method.
Pressure Transducers
Druck PDCR 1830-8335 (absolute)
Pressure transducers use electronic means (change in bridge resistance) to detect a pressure head due to the height of the water table (see Manufacturer Specifications for details). The supply voltage for Mn/ROAD is 2500 mV (2.5 volts), giving a full range output of 0 - 25 mV for 0-10 psi. The output from the transducer is an absolute value, meaning the output needs to be corrected for the affects of barometric pressure. Corrections to the data are made using the barometric pressure readings taken by the on-site weather station.
Data Collection and Processing
Pressure transducers are read every 15 minutes by a Campbell Scientific datalogger (CR10X). The output is in mV and is downloaded twice a day. The data is then loaded to the Mn/ROAD database daily. A database program for making the corrections for barometric pressure and conversion of mV to and elevation is pending the data quality check.
Data Quality
The data quality check consists of sampling the raw data and running through the manufacturer's calibration, and comparing these results to the manually collected data. Initially there appeared to be a barometric pressure affect on the sensor output even after making corrections for atmospheric pressure. After further investigation into errors associated with temperature, hysteresis, and supply voltage the conclusion was that fluctuations in the pressure transducer data, which can be seen particularly on cell 34, are most likely, if not entirely, due to transducer sensitivity. In the case of the Mn/ROAD pressure transducers, using a supply voltage of 2.5 Vinstead of 10V, amplifies the sensitivity inherent in the transducer (See manufacturers specification sheet: Application Data). The recommended supply voltage is 10V. We will probably increase the supply voltage in order to reduce errors.
Data Summary
Data are collected by the pressure transducers data collected manually from original standpipes located in the shoulder. The manual readings and the pressure transducer readings are in relative agreement. The greatest discrepancy between readings is in cell 34 where there is a difference of 1.2 ft. on a given day (see Table). Keep in mind that overlapping data is limited until all data is loaded into the database and processed.
Air Filled Coaxial Cable
One air filled coaxial cable is installed in each OS pipe along with a pressure transducer (see Fig). The coaxial cable is used to make TDR measurements of the water table depth. This method for measuring the water table depth may require less maintenance and be more rugged than using pressure transducers. The following summarizes the initial field data analysis, as well as the laboratory study conducted to verify the waveform analysis method.
In the Field
The water table depth measured by time domain reflectometry methods over estimated the height of the water table when compared to manual and pressure transducer readings. Initially the inflection point of the raw wave form was used to estimate the water depth. Using this method of analysis (Method 1, see below) to estimate the water depth produced a difference in water table depth by as much as 5 feet, when compare to standard methods of measurement. Therefore developing an algorithm that more accurately measures the water table depth was needed. To do this a laboratory experiment was conducted. A piece of air fill coaxial cable 5 feet long, and an electronic pressure transducer were used to measure various known water depths. A Campbell Scientific CR10X datalogger and Tektronix 1502B were used to automate the data collections. The results are shown below.
In the Lab
- Setting the propagation velocity (Vp) to the correct value is critical. The Vp should be set to the Vp of the hollow fill coax cable. This means that if there is a lead cable from the coax to the Tektronix, the apparent length of that cable should be entered into the cable length parameter of the Campbell TDR program instruction.
- An understanding of the Campbell Scientific dataloggers and execution of the programming instructions is required.
- Calculating the maximum of the first derivative can be easily automated using the Campbell datalogger. Automating the second derivative method will be coded into the database loader program.
The table below shows the laboratory results. The minimum of the second derivative produced an accurate measure of the water depth. The errors in initial measurements taken in the field were due to the Vp setting. The Vp in the field was set lower than what it should have been thus resulting in gross over estimations. The next step is to apply this analysis method to the field data.
Inches of Water |
Inches of Water |
1st Derivative (maximum) |
2nd Derivative (minimum) |
Error |
1st Derivative (maximum) |
2nd Derivative (minimum) |
Tape Measure |
Transducer |
Coaxial Cable |
Coaxial Cable |
Transducer |
Coaxial Cable |
Coaxial Cable |
0.0 |
0.0 |
-0.4 |
0.4 |
0.0 |
-0.4 |
0.4 |
6.0 |
6.4 |
5.1 |
5.9 |
0.4 |
-0.9 |
-0.1 |
9.0 |
9.3 |
8.3 |
9.0 |
0.3 |
-0.7 |
0.0 |
12.0 |
12.3 |
11.0 |
11.8 |
0.3 |
-1.0 |
-0.2 |
15.0 |
15.6 |
14.1 |
14.9 |
0.6 |
-0.9 |
-0.1 |
18.0 |
18.2 |
16.9 |
17.7 |
0.2 |
-1.1 |
-0.3 |
21.0 |
21.6 |
20.0 |
20.8 |
0.6 |
-1.0 |
-0.2 |
Method 2, finding the minimum of the 2nd derivative and it's associated point produced the most accurate measure of the water depth. TDR accuracy appears better than that of the pressure transducer.
Methods of Waveform Analysis:
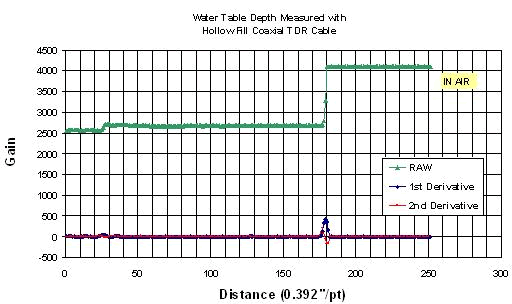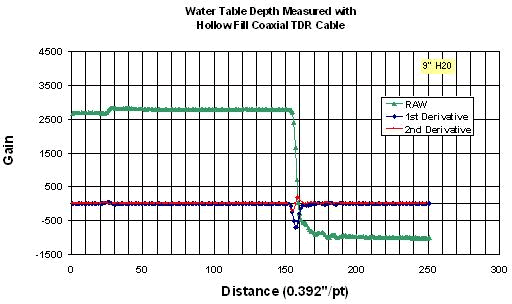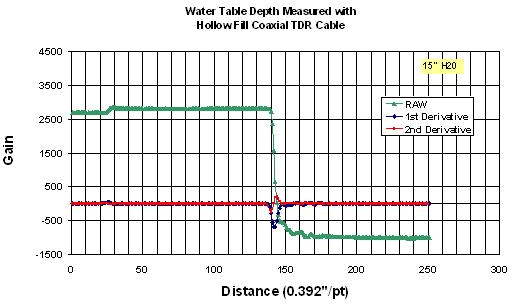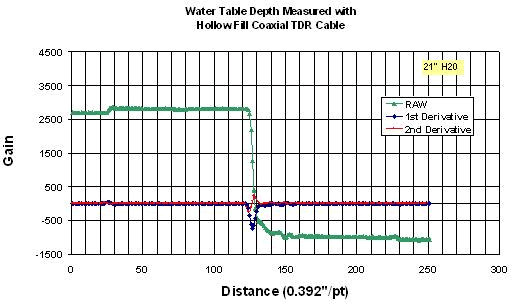
Method 1
Finding the local minima of the 1st derivative of the differential function dy/dx
min (f '(x) = dy/dx)
Method 2
Finding the local minima of the 2nd derivative of the differential function dy/dx
min (f ''(x) = dy/dx)


 MnPAVE Home
MnPAVE Home